백준 5626번 제단

< 백준 5626번 제단 - 마포 코딩박 >

 사용한 알고리즘: DP

 도둑이 일부 훔쳐간 제단의 상태가 주어지고, 해당 제단의 훔쳐가기 전 상태가 몇개나 가능한지 구하는 문제입니다.

문제풀이는 다음과 같습니다.

(1) (생각)
 0번째 제단열부터 N-1번째 제단열이 가능한 높이를 생각해보면 다음과 같습니다.
 0번째 제단열 : 높이 0 가능
 1번째 제단열 : 높이 0, 1 가능
 2번째 제단열 : 높이 0, 1, 2 가능
 ...
 k번째 제단열 : 높이 0, 1, 2, ... , min(k, (N-1)-k) 가능
 ...
 N-2번째 제단열 : 높이 0, 1 가능
 N-1번째 제단열 : 높이 0 가능
 k번째 제단열의 최대 높이는 제단 양끝 중 가까운 거리만큼 입니다.

(2) (코드 9~11)
 'dp[i][x] : i번째 제단열 높이가 x를 만족하는 경우수' 로 설정하였습니다.

(3) (코드 25~63)
 0번째 제단열 부터 N-1까지 탐색하며 dp값(높이별 경우수)을 구합니다. i번째 제단열의 높이별 dp값은 바로 전 i-1번째 제단열을 통해 구할 수 있습니다. 따라서 dp배열은 2개면 됩니다.
 i번째 제단열의 x높이는 i-1번째 제단열의 높이 x-1,x,x+1에서 만들 수 있음을 생각합니다.
 i번째 제단열의 높이가 정해진 경우는 해당 높이의 dp값만 계산하면 되고,
 i번째 제단열의 높이가 정해지지 않은경우 (도둑맞은경우) 가능한 높이의 dp값을 다 구해줍니다.

 사실 설명이 너무 어려워서 예를 들어보겠습니다.
문제의 예제 3,
input:
6
-1 -1 -1 2 -1 -1
로 주어졌을 경우입니다.

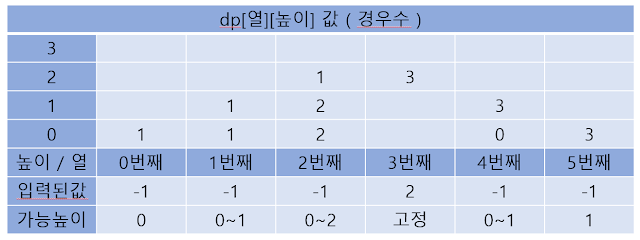
0번째 제단열은 가능높이가 0 이고, 이때 경우수는 1(초기값) 입니다.
1번째 제단열은 가능높이 0 : 0번째의 높이 0,1로 만들어짐 / 가능높이 1 : 0번째의 높이 0,1,2, 로 만들어집니다.
2번째 제단열은 가능높이 0 : 1번째의 높이 0,1로 만들어짐 / 가능높이 1 : 1번째의 높이 0,1,2 로 만들어짐 / 가능높이 2 : 1번째의 높이 1,2,3으로 만들어집니다.
3번째 제단열은 입력된 고정 높이 2 : 2번째의 높이 1,2,3으로 만들어집니다.
4번째 제단열은 가능높이 0 : 3번째의 높이 0,1로 만들어짐 / 가능높이 1 : 3번째의 높이 0,1,2로 만들어집니다.
5번째 제단열은 가능높이 0 : 4번째의 높이 0,1로 만들어집니다.
5번째 제단열이 마지막 열이므로 이 열의 높이 0 에 구해진 dp값(경우수)가 정답입니다.
이로써 주어진 조건의 6열짜리 제단열을 만드는 경우수는 3임을 알 수 있습니다.

굉장히 빈약한 설명이지만 찰떡같이 이해가 되셨기를 바라겠습니다...

	#include <bits/stdc++.h>
	using namespace std;
	const int MOD = 1e9+7;
	const int MAX = 1e4;
	int N;
	// arr[i] 의 최대 : min(i-0, (N-1)-i) : 양끝까지 거리
	int arr[MAX+1];
	// dp[i][x] : i 제단 열이 높이 x 를 만족하는 경우수 ( 2차원 그래프 그려보기 )
	// i번째 제단 열을 i%2 번째로 생각, 노드 값을 줄였다. (어차피 직전 제단만 본다.)
	int dp[2][MAX/2+1];
	int main(){ios_base::sync_with_stdio(false);cout.tie(NULL);cin.tie(NULL);
	cin >> N;
	for(int i=0; i<N; ++i){
	cin >> arr[i];
	// 애초에 불가능 한 경우 입구컷
	// i번째 열은 양끝중 가까운 거리 만큼만 올라갈 수 있음을 생각.
	if(arr[i] > min(i,(N-1)-i)){
	cout << 0 << '\n';
	return 0;
	}
	}
	// 초기값 설정
	dp[0][0] = 1;
	dp[1][0] = 1;
	for(int i=0; i<N; ++i){
	// i번째 제단 열을 i%2 번째로 생각, 노드 값을 줄였다. (어차피 직전 제단 열만 본다.)
	int idx = i%2;
	// 직전 제단
	int pre = (idx+1)%2;
	// dp[idx] 비우고 시작.
	for(int x=0; x<MAX/2; ++x) dp[idx][x] = 0;
	if(arr[i]==-1){
	// -1 이면 해당 열은 높이가 0~min(i,(N-1)-i) 까지 될 수 있다.
	for(int x=0; x<MAX/2; ++x){
	// 가능한 최대 높이까지만
	if(x>min(i,(N-1)-i)) break;
	for(int k=-1; k<2; ++k){
	int prex = x+k;
	// 음수높이 불가능
	if(prex<0) continue;
	dp[idx][x] += dp[pre][prex];
	dp[idx][x] %= MOD;
	}
	}
	}
	else{
	for(int k=-1; k<2; ++k){
	int prex = arr[i]+k;
	if(prex<0) continue;
	dp[idx][arr[i]] += dp[pre][prex];
	dp[idx][arr[i]] %= MOD;
	}
	}
	// 마지막 열에 정답이 모인다. (그래프 그려보면 확 보임)
	if(i==N-1) cout << dp[idx][0]%MOD << '\n';
	}
	return 0;
	}

view raw BOJ 5626.cpp hosted with ❤ by GitHub