백준 13430번 합 구하기

문제

S는 다음과 같이 정의된다.

• S(0, n) = n (모든 양의 정수 n)
• S(k, n) = S(k-1, 1) + S(k-1, 2) + ... + S(k-1, n) (모든 양의 정수 k, n)

k와 n이 주어졌을 때, S(k, n)을 1,000,000,007로 나눈 나머지를 구하는 프로그램을 작성하시오.

문제풀이

사용한 알고리즘 : 희소테이블

강산님의 블로그를 참고하여 풀이하였습니다.

(0) 생각

 S(k, n) = S(k-1, 1) + S(k-1,2) + ... + S(k-1,n) 을 아래 표로 생각해봅시다.

n    \    k	0	1	2	3	4
1	1	1	1	1	1
2	2	3	4	5	6
3	3	6	10	15	21
4	4	10	20	35	56
5	5	15	35	70	126

 잘 생각해보면,

 S(k, n) = S(0, n) + S(1, n-1) + S(2, n-1) + ... + S(k, n-1) 을 알 수 있습니다.

 예를 들어 S(4, 5) = S(0, 5) + S(1, 4) + S(2, 4) + S(3, 4) + S(4, 4)

                       = 5 + 10 + 20 + 35 + 56 = 126  입니다.

 여기서 조금만 더 생각하면 S(0, n) = 1 + S(0, n-1) 이지요.

 따라서 S(k, n) = 1 + S(0, n-1) + S(1, n-1) + ... + S(k, n-1) 입니다.

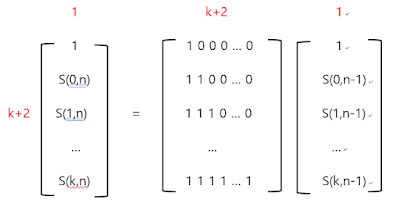
 이를 행렬로 표현해보면 다음과 같습니다.

 

 우변의 lower-triangle matrix ( 대각선 이하 1인 행렬 ) 을 A라 하면, A 는 (K+2) x (K+2) 행렬이고,

 

  임을 알 수 있습니다.

 이때, S(0,1) = S(1,1) = ... = S(k,1) = 1 이므로,

 결국 A^n-1 의 마지막 행을 구하는 문제가 됩니다.

(1) 코드 48~53

 위에서 언급한, (K+2) x (K+2) 행렬 A 를 만들어줍니다.

 행렬은 벡터로 생각해줄 것입니다.

 예를 들어 행렬의 (i,j) 원소는 벡터에서 i*(K+2) + j 의 index를 갖습니다.

(2) 코드 19~37

 행렬 곱을 구현하는 함수를 하나 만들어줍니다.

 행렬 곱이 어떻게 작동하는지 생각해보면... 됩니다.

(3) 코드 55~60

 희소테이블로 A^n-1 을 구해줍니다.

 

(4) 코드 62~67 

 구해진 A^n-1 의 마지막 행을 다 더한 것이 답이 됩니다.
 

(5) 주의

 N=1 로 입력이 주어질 때, 과정(3) 의 while문은 돌아가지 않습니다.

 따라서 제 코드에 따르면 A^n-1를 저장하는 벡터가 비어있게 됩니다.

 생각해보면, N=1 로 주어지면 S(K, 1) = 1 이므로 그냥 1 을 출력해주면 됩니다.

	#include <bits/stdc++.h>
	using namespace std;
	typedef long long ll;
	const ll MOD = 1000000007;
	// n\k 그래프 그려보기! ( 강산님 점화식 참고 )
	// S(k,n) = S(k-1,1) + ... + S(k-1,n)
	// = 1 + S(0, n-1) + S(1,n-1) + ... + S(k-1, n-1)
	// 이걸 '행렬' 로 조지기...! lower triangular (원소는 1)
	int K, N;
	// lower triangular(원소는 1)
	// k+2 x k+2 행렬 ( 1 들어가고 S(0, n) ~ S(k,n) 들어가야하니 )
	// 이걸 n-1 승 할꺼임
	// {1, S(0,n), S(1,n), ... , S(k,n)}^T = A^n-1{ 1, S(0,1), ... , S(k,1)}^T
	// = A^n-1{1, 1, ... , 1}^T (transpose)
	vector<int> A;
	vector<int> ans;
	vector<int> Square(vector<int> V1, vector<int> V2) { // 행렬 곱
	if (V1.empty()) return V2;
	vector<int> ret;
	for (int i = 0; i < K + 2; ++i) {
	for (int j = 0; j < K + 2; ++j) {
	ll r = 0LL;
	for (int k = 0; k < K + 2; ++k) {
	int a1 = i * (K + 2) + k; // i 행
	int a2 = k * (K + 2) + j; // j 열
	r += 1LL*V1[a1] * V2[a2];
	r %= MOD;
	}
	ret.push_back((int)r);
	}
	}
	return ret;
	}
	int main() {ios_base::sync_with_stdio(false); cout.tie(NULL); cin.tie(NULL);
	cin >> K >> N;
	// N 을 1 주면 위에 while문이 안돌아갈 수 있음. S(k,1) = 1을 미리 처리해주자
	if (N == 1) {
	cout << 1 << '\n';
	return 0;
	}
	for (int i = 0; i < K+2; ++i) { // 크기 k+2 개
	for (int j = 0; j < K+2; ++j) {
	if (j <= i) A.push_back(1); // lower triangle
	else A.push_back(0);
	}
	}
	N--; // N=1 일때 미리 처리해줌. 안그러면 while문 안돌아서 ans 가 비어버림
	while (N) {
	if (N % 2) ans = Square(ans, A);
	A = Square(A, A);
	N /= 2;
	}
	int result = 0;
	// 마지막 행 K+2 개 더하기
	for (int j = 0; j < K + 2; ++j) {
	result += ans[(K + 1) * (K + 2) + j];
	result %= MOD;
	}
	cout << result << '\n';
	return 0;
	}

view raw BOJ 13430.cpp hosted with ❤ by GitHub