백준 17236번 Heights
문제
삼각형의 각 점에서 반대편 변에 대해서 수선을 그어보자. 각 수선의 길이는 그 삼각형의 높이라고 할 수 있을 것이다.
각 점에서 반대편 변에 수선을 그어 구한 삼각형의 높이 값 3개가 주어진다. 이 삼각형의 넓이를 구하여라.
문제풀이
사용한 알고리즘 : 수학, 이분탐색
(0) 수학
세 변 a, b, c에 대응되는 높이를 h_a, h_b, h_c라 하면 S는 다음과 같겠죠.
따라서 넓이와 각 대응되는 높이를 안다고 한다면, 세 변을 다음과 같이 생각할 수 있습니다.
우리가 쓸 헤론의 공식은 다음과 같습니다. (자세한건 링크 : 헤론의 공식 )
세 변을 a, b, c에 대해 t = (a+b+c)/2 라 하면 넓이 S는 다음과 같습니다.
(1) 생각
세 높이는 입력으로 주어졌습니다.
이분탐색을 통해 적절한 넓이를 구할 것입니다.
넓이를 X라 추정한다면, 주어진 세 높이와 X를 통해 세 변 a,b,c를 구할 수 있습니다.
이후 구한 세 변을 갖고 헤론의 공식을 활용하여 넓이 X' 을 역으로 구해봅니다.
잘 생각해보면 X 와 X' 사이의 관계에 따라 다음과 같이 생각 가능합니다.
1. X = X' 인 경우 해당 추정 넓이가 구하고자 하는 답입니다.
2. X > X' 인 경우 X를 더 크게 잡아야 합니다.
3. X < X' 인 경우 X를 더 작게 잡아야 합니다.
(2) 코드 16~19
세 변이 주어졌을 때 헤론의 공식으로 삼각형의 넓이를 구하는 함수입니다.
(3) 코드 21~31
X 라고 넓이를 추정하였을 때, 과정(1)에서 생각한 조건 1,2,3 중 어느 경우인지 판단해주는 함수입니다.
|X-X'| < 0.0000001 일 경우 X=X' 라고 판단하였습니다.
(4) 코드 37~50
이분탐색을 통해 적절한 넓이를 찾는 코드입니다.
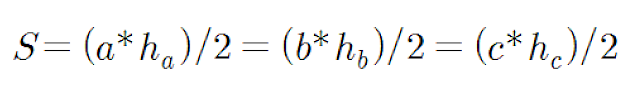



댓글
댓글 쓰기
긴 글 읽어주셔서 감사합니다.
궁금한게 있으시다면 댓글 달아주세요!